寻找一棵普通二叉树(非二叉搜索树)的最近公共祖先。
输入空间:二叉
解空间:二叉
解题“七步走” (保持这种sense):
- 题意 Scenario
- 假设 Assumptions
- 举例与输入输出 Examples and figure out Input/Output
- 思路(什么数据结构, 什么算法)Thinking Process (What data structure, algorithm?)
- 代码 Coding
- 复杂度分析 Complexity Analysis
- 测试 Tests
题目要求
原题链接
寻找一棵二叉树的两个节点的最近公共祖先。
最近公共祖先的定义是:在给定的二叉树中,对于给出的两个节点p和q,最近公共祖先A是能满足p和q皆为A的子节点,且A是在从上到下的层次关系中最靠近p和q的节点。(言下之意,本定义也允许A是p或q节点中的一个)
假设
面试者:我们能假设该二叉树中没有相同数值的节点吗?
面试官:可以。
面试者:我们能假设该给出的p和q节点,p的值一定小于q吗?
面试官:不可以。
举例与输入输出
例子直接用LeetCode上的图。
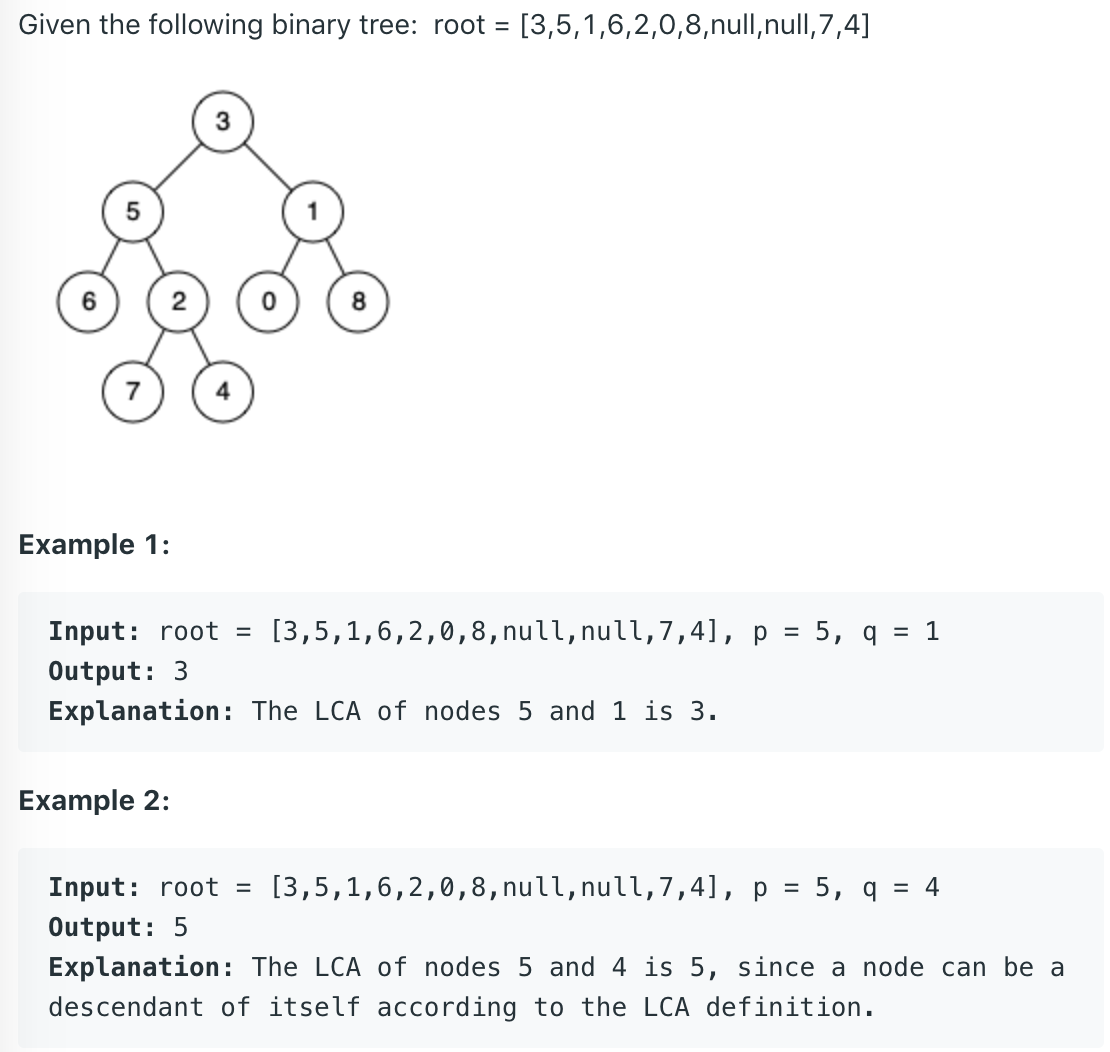
在例子1中,节点5和1的最近公共祖先就是全局的根节点3。在例子2中,节点5和4,由于5刚好是4的父节点的父节点(祖父节点),所以5和4的最近公共祖先就是节点5。
思路:分治法
由于这道题与LC 235寻找二叉搜索树的最近公共祖先很接近,但差异就在于二叉搜索树的每个节点之间始终符合左<中<右的模式,而本题的普通二叉树不具备这种模式。所以,本题就不能通过节点之间的值比大小来求解,而要通过分治法。
在分治法的分的过程中,我们要把当前根的左节点或右节点,与目标节点p和q分别代入到下一个子问题当中去。
与LC 235类似的是,本题中的最近公共祖先与目标节点p和q的关系,恰好也分为下述三种情况,我给大家画一画:
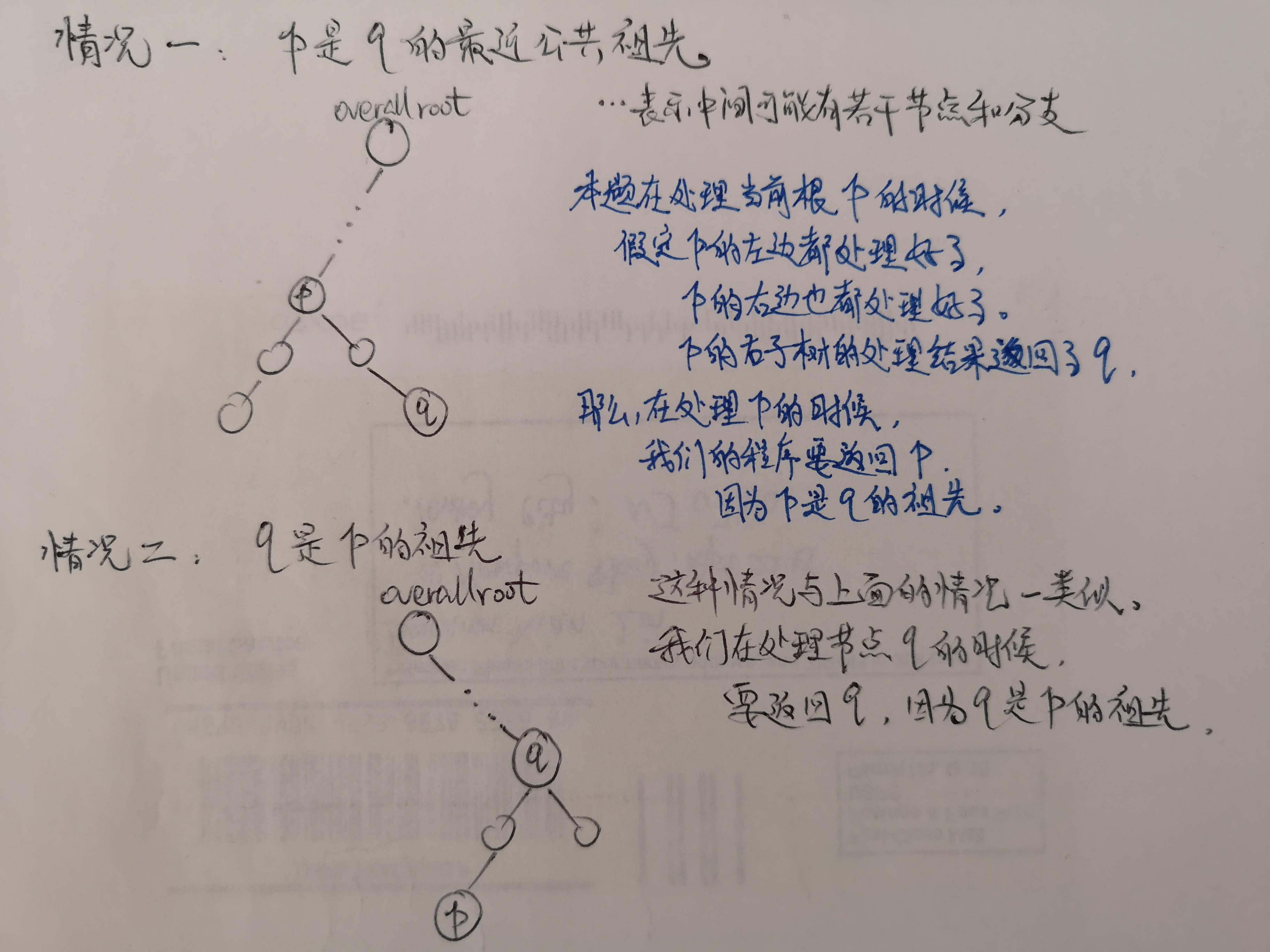
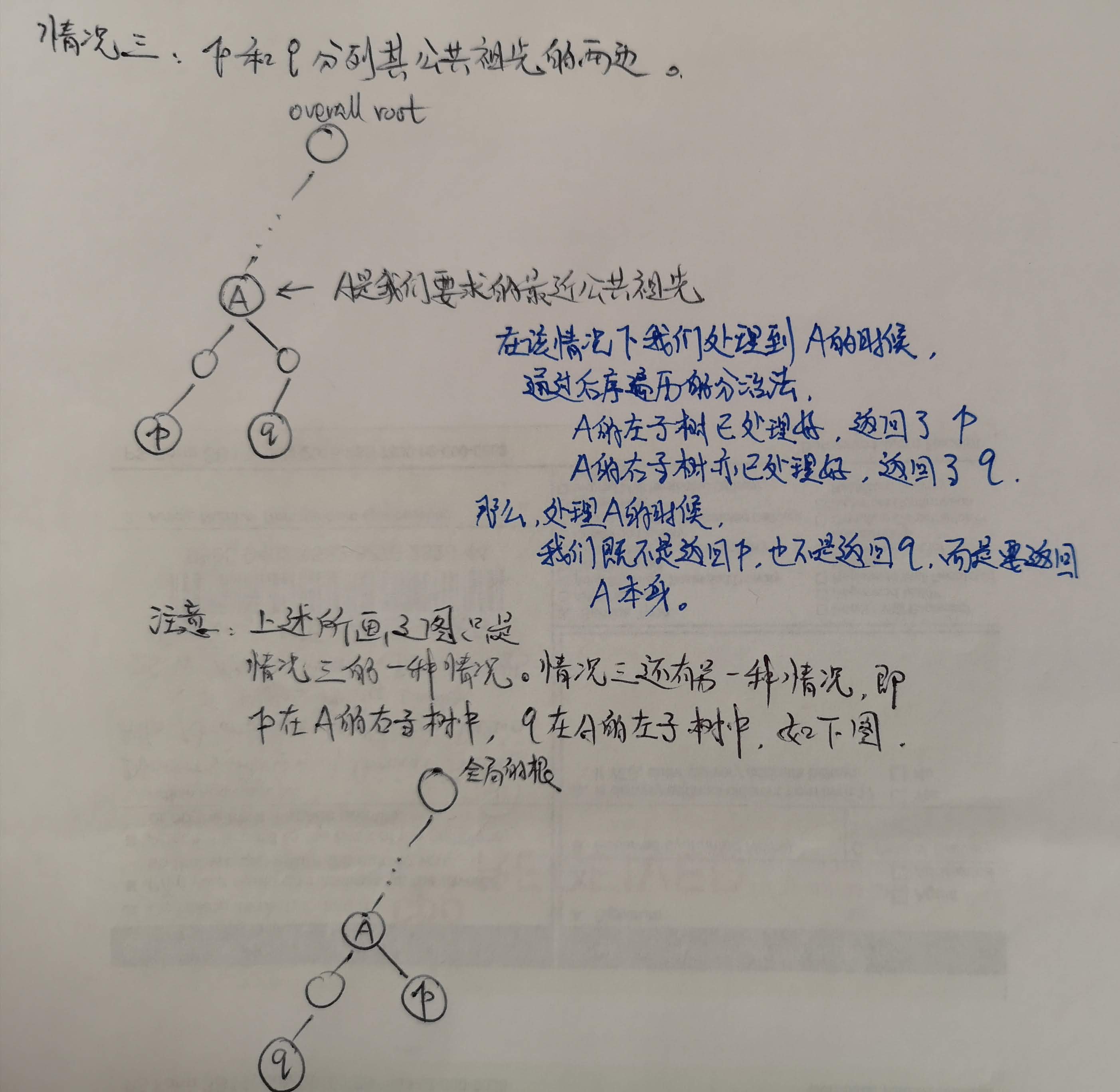
本题的分治法从后序遍历的思想入手比较容易思考,即我假定当前根的左子树都处理好了,右子树都处理好了,现在面对当前根的时候,我应该返回什么。
本题(LC 236)代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// Base case: 走到底(叶节点之下)了
if (root == null) {
return null;
}
// 第一、二种情况
if (root == p || root == q) {
return root;
}
// Divide
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
// 第三种情况
if ((left == p && right == q) || (left == q && right == p)) {
return root;
}
// 最后还要考虑,我们要求的最近公共祖先
// 它可能在处理到当前根的左子树时就已得出正确答案要返回,
// 也有可能在处理当前根的右子树时已得出正确答案要返回
if (left != null) {
return left;
}
return right;
}
}
代码优化
上面的代码已经是正确答案,但我们还有优化的空间。
首先,走到底的base case与第一、二种情况,都是可以并到一起写,返回return root就可以了。
其次,第三种情况左子树能返回的结果,要么是p要么是q,不会有别的情况,右子树也类似。所以,只要写成if (left != null && right != null)就可以了。
最后,处理要么在左子树就得到正确答案或者在右子树就得到正确答案的时候,可以把它写成一个三项表达式,即
return left != null ? left : right;
整理后的代码如下:
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null || root == p || root == q) {
return root;
}
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if (left != null && right != null) {
return root;
}
return left != null ? left : right;
}
}
把上述代码贴到LC OJ(LeetCode Online Judge),看看效果如何。
时间空间复杂度
时间复杂度:由于要遍历二叉树的所有节点,所以O(n),
空间复杂度:为递归栈的深度,所以是O(log(n))。