LeetCode 437. Path Sum III

二叉树的路径和 III – 找出满足二叉树的路径和的所有路径的个数，这一次路径的定义不必起始于全局的根，也不必结束于叶子节点。

输入空间：二叉
解空间：二叉

解题“七步走” (保持这种sense)：

题意 Scenario
假设 Assumptions
举例与输入输出 Examples and figure out Input/Output
思路（什么数据结构，什么算法）Thinking Process (What data structure, algorithm?)
代码 Coding
复杂度分析 Complexity Analysis
测试 Tests

题目要求

原题链接
给定一个二叉树，二叉树的每个节点带整数数值，可正可负。找出能使得路径上的节点的值加起来等于目标和的这样的路径的个数。注意，本题的路径的定义是，可以从二叉树的任何一个节点开始，向下方走到某个节点，就算本题所指的路径。所以，路径的开始点不必是全局的根，结束点也不必是叶节点，但一定是向下方走，即从一个父节点走到一个子节点。

再给一个假设就是，给定的二叉树的总节点数<=1000个，每个节点的值的取值范围是[-1e6, +1e6]。1e6即为100万的科学计数法表示。

假设

本题的假设在于，面试者需要和面试官确认清楚“路径”的定义。还有就是：
面试者：单个节点刚好等于目标和，这单个节点算一个满足的路径吗？
面试官：算。

举例与输入输出

例子直接用LeetCode上的图，还是很好理解的。

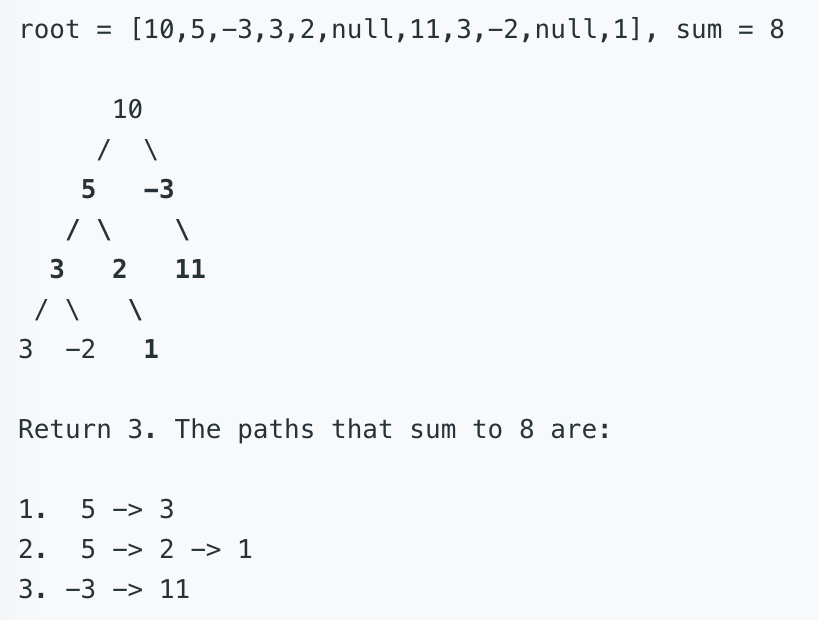
oh-my-zsh

在本例子中，有3条路径是满足的。从左边的那个节点5开始有两条，5->3与5->2->1。其中5->3就属于形成路径的初始和结束的两个节点既不是全局的根，也不是叶节点的情况。5->2->1是结束在了叶节点。右边的话有一条，即-3->11。总体有3条满足的，函数返回数字3就可以了。

思路: 渐变法–如何改造已做过的题目，渐变出我们想要的答案

想想，我们上期讲的是LeetCode 113. Path Sum II，问的是找出所有满足从全局的根开始直到某个叶节点结束的路径，使得该路径节点的值的和与目标和相等。

那么，本期这个题目，我们就来看看在思考过程中，如何先给题目降低难度，逐步靠上已经做过的题，从而得到最终的解答。

本期这个题，路径的定义是从任意节点开始，我们的第1步降低难度是：

“假定我现在要求路径是必须从全局的根开始，向下遍历结束于任一节点，使得路径和规则得以满足，这样的路径有几条？”（第1步降低难度题）

通过第1步的降低难度，我们接近了我们曾做过的LC 113题目，但还差一点，那我们再来第2步的降低难度，规定：

“假定我现在要求路径是必须从全局的根开始，向下遍历结束于某个叶节点，使得路径和规则得以满足，这样的路径有几条？”（第2步降低难度题）

这个问题是不是基本上就是LC 113的问题了？只不过LC 113是要列举出所有的路径，而这个问题只要return符合条件的路径的个数就可以了，免去了你需要开一个List of List变量存结果以及回溯的麻烦。

这里再贴一下LC 113的题目的例子截图，帮读者回忆下：

oh-my-zsh

根据第2步降低难度题的要求，我们只需要返回数值2就可以了，因为上图中符合要求的路径共两条。

那我们一步步来，首先先上LeetCode 113. Path Sum II的答案代码

class Solution {
  public List<List<Integer>> pathSum(TreeNode root, int sum) {
      List<List<Integer>> res = new ArrayList<>();
      List<Integer> tmp = new ArrayList<>();
      dfsSum(root, sum, tmp, res);
      return res;
  }
  public void dfsSum(TreeNode root, int sum, List<Integer> tmp, List<List<Integer>> res) {
      if (root == null) {
         return;
      }
      tmp.add(root.val);
      if (root.left == null && root.right == null && root.val == sum) {
         res.add(new ArrayList(tmp));
      }

      dfsSum(root.left, sum - root.val, tmp, res);
      dfsSum(root.right, sum - root.val, tmp, res);
      tmp.remove(tmp.size() - 1);
  }
}

通过改造LeetCode 113. Path Sum II的答案代码，获得第2步降低难度题的解法，如下：

class Solution {
  public int pathSum(TreeNode root, int sum) {
      return dfsSum(root, sum);
      /* 其实第2步降低难度题不需要用到辅助函数dfsSum()的写法，
      但为了展示每个降低难度的问题到最终问题的代码的渐变过程，保留这种写法。*/
  }
  public int dfsSum(TreeNode root, int sum) {
      /* Base case 1:
      若根为空了且没有满足要求，则符合的路径数目不增加，返回0 */
      if (root == null) {
         return 0;
      }

      /* 用count变量记录当前这个递归状态的符合的路径数，初始为0 */
      int count = 0;

      /* Base case 2:
      走到了叶节点，且发现形成的路径满足题目要求，count设为1 */
      if (root.left == null && root.right == null && root.val == sum) {
         count = 1;
      }

      // Divide
      int left = dfsSum(root.left, sum - root.val);
      int right = dfsSum(root.right, sum - root.val);

      // Conquer过程：把记录到的符合的路径数目累加起来
      return count + left + right;
  }
}

代码讲解尽在注释中。

搞定了第2步降低难度题，我们现在可以来对付第1步降低难度题了。第1步降低难度题的要求是：

“假定我现在要求路径是必须从全局的根开始，向下遍历结束于任一节点，使得路径和规则得以满足，这样的路径有几条？”

其实，向下结束于任一节点，比结束于叶子节点更简单了，主要把👆的代码加一丁点改动就行了，请读者自行观察，看看改动了哪里。

第1步降低难度题的解法，如下：

class Solution {
  public int pathSum(TreeNode root, int sum) {
      return dfsSum(root, sum);
  }
  public int dfsSum(TreeNode root, int sum) {
      if (root == null) {
         return 0;
      }

      int count = 0;

      /* Base case 2:
      向下遍历走到了某一节点，且发现形成的路径满足题目要求，count设为1 */
      if (root.val == sum) {
         count = 1;
      }

      int left = dfsSum(root.left, sum - root.val);
      int right = dfsSum(root.right, sum - root.val);

      return count + left + right;
  }
}

OK。搞定了第1步降低难度题，我们就可以来对付LC 437了。我们发现，LC 437与第1步降低难度题的唯一差别就在于，LC 437中的根是移动着的，它可以是整棵二叉树的全局的根，也可是它的子树的根。这也不难，根据我们先前做了好几遍的前序遍历的分治法，只要通过分治法让根的情况“动起来”就可以了。具体代码如下：

本题（LC 437）代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
  public int pathSum(TreeNode root, int sum) {
    if (root == null) {
      return 0;
    }

    // 通过分治法考虑根不为全局根的时候的情况
    int left = pathSum(root.left, sum);
    int right = pathSum(root.right, sum);

    return dfsSum(root, sum) + left + right;
  }

  private int dfsSum(TreeNode root, int sum) {
    if (root == null) {
      return 0;
    }

    int count = (root.val == sum) ? 1 : 0;

    int left = dfsSum(root.left, sum - root.val);
    int right = dfsSum(root.right, sum - root.val);

    return count + left + right;
  }
}

时间空间复杂度

时间复杂度：
这道题不仅仅是从全局的根开始遍历整个树的节点那么简单（暗示时间复杂度不太可能是O(n)）。的确，针对全局的根而言，算法要遍历n个节点。那么然后呢，针对全局根的左子树和右子树形成的两个子树，算法要遍历(n-1)个节点。再往下，算法要遍历(n-3)个节点。所以算法总共要遍历的节点数，大体上是一个等差数列求和
n + n-1 + n-3 + ...
所以是其数量级是n^2的，时间复杂度为O(n^2)。
当然，我这里没有给出严格的数学证明，如果有读者朋友通晓这个，欢迎评论留言，谢谢。

空间复杂度：为递归栈的深度，所以是O(log(n))。

互动问题

本题题目中的二叉树的节点个数(<=1000个)，以及每个节点的值的取值范围[-1,000,000 to 1,000,000]，对本题的解答究竟有何影响？欢迎评论留言发表您的看法。

LeetCode 437. 二叉树的路径和 III