做了一些题目,觉得自己有必要追本溯源,厘清一些更根本的概念性问题。所以,这一期推一篇讲解时间复杂度和空间复杂度的文字。之后会陆续推一些我个人的对数据结构和算法的理解的总括性文章,敬请期待。
时间复杂度
算法的时间复杂度能反映出程序运行从开始到结束所需要的时间,但并不是严格意义上指程序运行从开始到结束所需要的时间。因为即便是同一段程序,在不同的机器上或者网络环境下运行,其消耗的具体时间往往是不同的。但是,我们又需要比较完成同一个任务的不同的程序写法的运行效率。所以,更准确的对算法的时间复杂度的理解,可以是:
时间复杂度是算法运行时间与输入数据量的函数关系。
一般在北美的面试算法中,我们只考虑Big O(big oh)的时间复杂度关系,即通常取运行时最坏情况的时间消耗。
常见的时间复杂度
-
O(1)
这是指算法的运行时间不因为数据输入量的变化而变化,保持着一个常数时间。
常见的例子有:哈希表中的查找。 -
O(logN)
算法的运行时间与数据输入量对数关系。
常见的例子有:有序数组的二分查找,二叉搜索树的查找、插入、删除。 -
O(N)
算法的运行时间与数据输入量呈线性相关。
常见的例子有:无序数组的查找。 -
O(N*logN)
通常出现的情况是:O(logN)的操作执行了N次 或者 O(N)的操作执行了logN次。
常见例子:归并排序,快速排序(其中对快速排序,我们不是考虑其最坏情况而是看其均摊的时间复杂度)。 -
O(N^2)
算法的运行时间与数据输入量呈平方关系。
常见的例子有:冒泡排序、选择排序、插入排序。 -
O(2^N)
指数关系。低效的时间复杂度,应尽力避免。
常见的例子有:斐波那契数列的递归解法。 -
O(N!)
阶乘关系,是比指数关系更低效的时间复杂度,更应尽力避免。
常见的例子有:Permutation (比如求一组字母的全排列)。
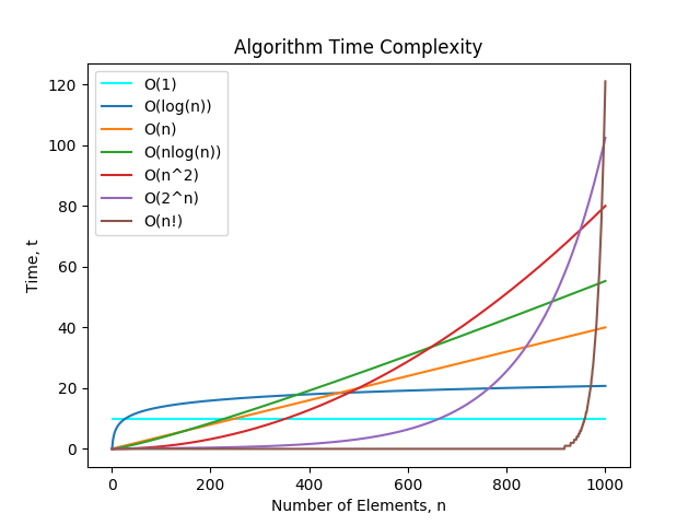
我们可以看看一张囊括上述几种时间复杂度的函数图。图中,横坐标为输入数据量,纵坐标为消耗时间。
空间复杂度
类似的,空间复杂度可以理解为:
算法运行空间 与 输入数据量 的函数关系。
它主要能反映出运行完一个程序所需内存的大小。利用程序的空间复杂度,可以对程序的运行所需要的内存多少有个预先估计。
在北美的算法面试中,描述一道题的空间复杂度有时候是有点儿tricky的。一道题的最终结果所要存储的空间,是否应当算入时间复杂度呢?这个,需要你在面试的时候跟面试官讨论,讲清楚。如果面试官说不算入,那么,你就只要考虑解这道题的过程中所要用的额外辅助空间,不考虑存储最终结果所要用到的空间,就行了。
以后,如果无特别标注,笔记哥的每个解题报告所谈的空间复杂度,都是只考虑程序运行过程中所要用的额外辅助空间,不考虑存储程序运行的结果所需要占用的空间。
勘误
- 笔记哥的LeetCode第104题解题报告
笔记哥原本是写空间复杂度,由于仅新开两个整数类型的变量left right来存中间计算的深度的结果,所以空间复杂度为O(1)。
这是不对的。
固然,我的解法是开了两个变量,但是,更重要的对于求二叉树的深度的这道题目,或者说对于很多二叉树类的题目,空间复杂度要考虑程序运行过程中的递归栈的深度,递归栈的深度,递归栈的深度!重要的事情说3遍。
什么是递归栈的深度呢?假定我们看下面这棵二叉树
3
/ \
9 20
/ \
15 7
在求最大深度的过程中,函数的自我调用过程(即递归过程)会把函数参数(parameter)放到内存的栈里。对于要算到3-20-15或者3-20-7所形成的深度,这个自我调用过程会使得内存的栈至少会放入 3, 20, 7 这三个节点。所以,内存栈会存放的最大节点数目为log(n),n为这棵二叉树的总的节点数。
所以,这道题的空间复杂度应当为O(log(n)), 或者你写做O(h) h–为树的深度,也可以。
- 笔记哥的LeetCode第144题 LeetCode第145题解题报告
在这两题的解题报告的结尾,我原本写道:空间复杂度,由于新开了一个变量用于存所有节点的值的res,所以空间复杂度为O(n)
这两道题假如“考虑存储最终结果所要用到的空间”,O(n)的空间复杂度肯定是对的。但假如我们按照今天这篇推文的新规则,或者说北美算法面试的比较主流的原则,“只要考虑解这道题的过程中所要用的额外辅助空间,不考虑存储最终结果所要用到的空间”的话,那么,这两道题的空间复杂度就应当是O(log(n))。 原因嘛,跟上面的递归栈的例子是一样的。