看看不同类型的二叉树的中美差异

在面试中，我们会遇到不同类型的二叉树。碰巧，美国英文语境下的一些二叉树类型与中国中文语境下的对应翻译有匹配不当之处（mismatch）。本文试图做一个归纳整理，方便身处两个国家的小伙伴们在面试遇到二叉树类算法题的时候，不至于因为语境下的定义不同而吃亏。

根据笔记哥亲身经历，本文先描述美国语境下的一些二叉树类型的定义，再描述中国语境下的，最后再做一个小结。

注：由于下面提到的二叉树类型不包括二叉搜索树（Binary Search Tree），所以虽然树的每个节点都带有数字，但只是为了叙述方便，您可以着重看节点的位置、数量、分布等信息对二叉树的类型加以区别。

英语语境

美国语境下对于二叉树类型的定义，取材自维基百科与GeeksforGeeks这两个网站。

Full Binary Tree

Full Binary Tree 的英文定义是：A Binary Tree is full if every node has 0 or 2 children (source: GeeksforGeeks)。翻成中文就是：一个二叉树的任何一个节点，如果包含0个或者2个子节点的话，那么这个二叉树即为“满二叉树”。

下面这个例子是一个Full Binary Tree (满二叉树)

因为每一个节点要么包含两个子节点，要么包含0个子节点，并没有出现某一个节点只包含1个子节点的现象，所以是Full Binary Tree (满二叉树)。

下面这个例子还是一个Full Binary Tree (满二叉树)

            18
        /        \  
       15        30  
      /  \       /  \
    40    50    100   40

这不单是一个Full Binary Tree的例子，而且还是一个Perfect Binary Tree（完美二叉树）的例子，我们下面会讲到。

下面这个例子就不是一个Full Binary Tree (满二叉树)

因为在这个二叉树中，节点15只有一个子节点40，没有右子节点，所以整个树不是一个Full Binary Tree (满二叉树)。

Full Binary Tree有一个重要属性：如果我们把所有内在的节点的个数记做大写的I，把所有的叶子节点的个数记做大写的L；那么，我们有L = I + 1。

Complete Binary Tree

Complete Binary Tree 的英文定义是：A Binary Tree is complete Binary Tree if all levels are completely filled except possibly the last level and the last level has all keys as left as possible (source: GeeksforGeeks)。翻成中文就是：如果一个二叉树，除了最下面一层外，其他所有层都铺满节点，且最下一层的所有节点都是从最左边开始排开，那么该二叉树就是一个“完全二叉树”。

看一个完全二叉树的例子：

             18
          /       \  
        15         30  
       /  \        /  \
     40    50    100   40
    /  \   /
   8   7  9

再看一个不是完全二叉树的例子：

             18
          /       \  
        15         30  
       /  \        /  \
     40    50    100   40
    /  \     \
   8   7      9

在这个二叉树中，节点50下属的叶节点位于整个树的最下一层；但50的左节点没有被填充，反而是它的右节点被填充了9，所以该二叉树不是Complete Binary Tree (完全二叉树)。

Perfect Binary Tree

Perfect Binary Tree 的英文定义是：A Binary tree is Perfect Binary Tree in which all internal nodes have two children and all leaves are at the same level. (source: GeeksforGeeks)。翻成中文就是：如果一个二叉树，所有的内在节点都有两个子节点，且所有的叶子节点都在同一层，那么该二叉树就是一个“完美二叉树”。

看一个Perfect Binary Tree（完美二叉树）的例子：

             18
          /       \  
        15         30  
       /  \        /  \
     40    50    100   40

重要规律：

一个Perfect Binary Tree（完美二叉树）一定是一个Full Binary Tree（满二叉树），反之不一定成立。
一个Perfect Binary Tree（完美二叉树）一定是一个Complete Binary Tree（完全二叉树），反之不一定成立。

中文语境

中文维基百科中提到的满二叉树（Full Binary Tree）

中文维基百科关于“二叉树”的页面为：https://zh.wikipedia.org/wiki/%E4%BA%8C%E5%8F%89%E6%A0%91
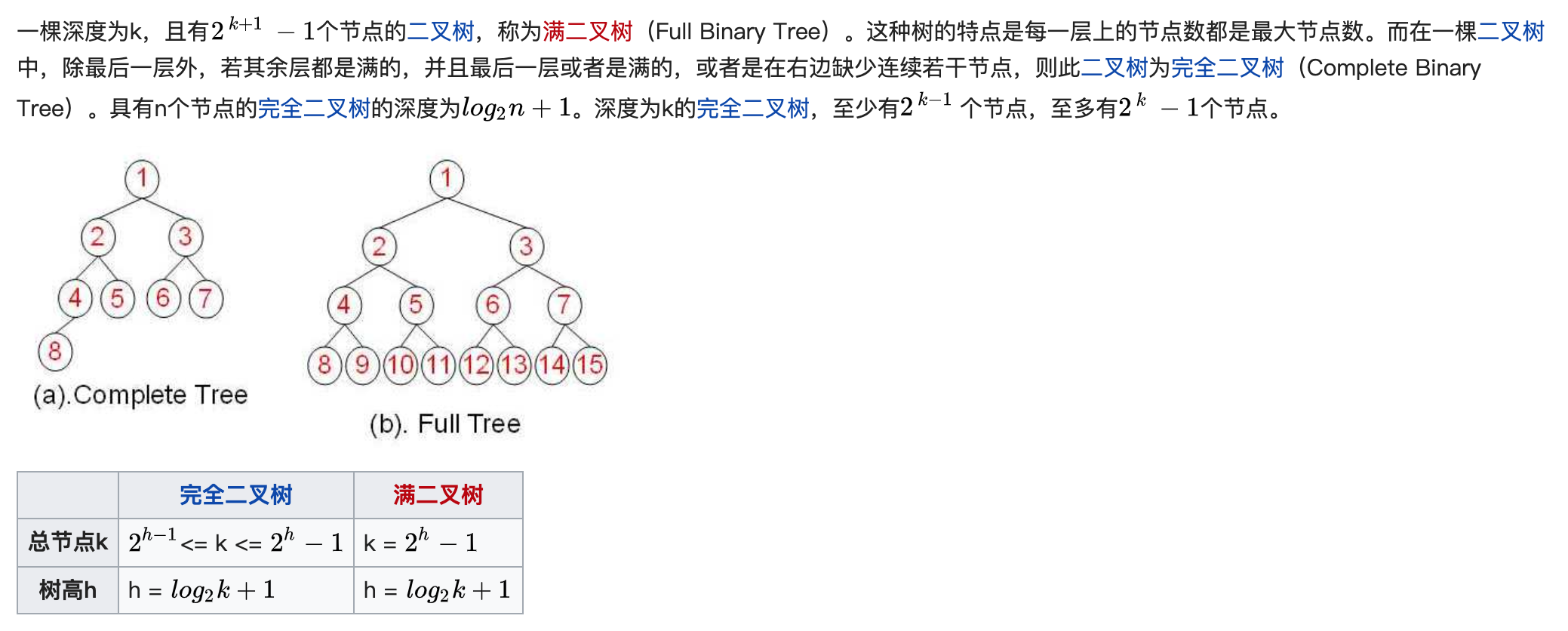
我是在美东时间2019年8月24日下午1点44分访问的，截图如下： oh-my-zsh

这个中文维基百科页面对于二叉树中的“满二叉树”的定义，与我们上面提到的英文语境中的Full Binary Tree（满二叉树）的定义是不同的，具体可以看看这句话：

一棵深度为k，且有2^(k+1) - 1个节点的二叉树，称为满二叉树（Full Binary Tree）。

这个定义中，树的层数是从0开始数的，即只有一个根的树，它的深度为0，它的节点数自然就是2^(0+1)-1 = 1个节点。

那么，按照这个定义，原先在英文语境中符合Full Binary Tree（满二叉树）的这个例子：

其节点总是为5个，并不等于2^(k+1)-1 = 2^(2+1)-1 = 7个，所以就不是中文语境下的“满二叉树”了。This is the tricky part! (这就是容易造成混淆的地方！)

我们也容易看出，其实这个中文语境里的“满二叉树”，因为要求树的总节点数为2^(k+1)-1，其实就是对应了英文语境中的 Perfect Binary Tree（完美二叉树）。我们再看看这个完美二叉树的例子，

             18
          /       \  
        15         30  
       /  \        /  \
     40    50    100   40

是不是就符合总节点数 = 2^(k+1)-1 = 2^(2+1)-1 = 7个了呢。

归纳小结

综上，英中语境对二叉树的类型的理解，容易混淆的就是英文语境中的 Full Binary Tree (满二叉树)， Perfect Binary Tree（完美二叉树） 与中文语境中的 满二叉树。

我在现阶段的基本概括就是：

英文语境中的 Perfect Binary Tree（完美二叉树） 可以与中文语境中的 满二叉树 划等号。
似乎，中文语境中目前没有一个标准的，对英文语境中的 Full Binary Tree (满二叉树) 的术语称谓。

好在，我们程序员大都是务实的、讲定义、讲逻辑的人。不论是美国英语语境还是国内中文语境，在面试的时候，你都可以就定义问题事先跟面试官做好沟通，确认好你所理解的题目中的二叉树类型的定义是否是面试官她心目中的二叉树类型的定义，就可以确保在定义问题上，万无一失了。

不单单是做题目，在跟队友、同事、同学讨论技术问题的时候，也要学会首先确保在问题的定义上达成一致，然后才继续讨论，否则就会有鸡同鸭讲、浪费时间的风险喽。

另附：如果读者朋友发现本文有什么漏洞，或者是觉得有什么相似的二叉树类型的面试题相关内容希望笔记哥今后写到，都可以留言让我看到，谢谢。

Different Types of Binary Trees