回顾
解题“七步走” (保持这种sense):
- 题意 Scenario
- 假设 Assumptions
- 举例与输入输出 Examples and figure out Input/Output
- 思路(什么数据结构, 什么算法)Thinking Process (What data structure, algorithm?)
- 代码 Coding
- 复杂度分析 Complexity Analysis
- 测试 Tests
题目要求
原题链接
给你一棵二叉树,找出它的最大深度。最大深度的定义是:一棵二叉树沿着它的最长的路径一直到叶节点,所形成的深度。
假设
询问面试官,树的最大深度的一个细节定义。假如一棵树只有一个节点(根节点)的话,它的深度是算0还是1?(因为程序员数数很多时候从0开始)。
面试官回答:算1。则你明确了树的深度的定义和初始值,可以继续。
举例与输入输出
3
/ \
9 20
/ \
15 7
那么,我们要得到的结果就应是3,深度沿着的是从3->20->15 或 3-20->7的路径。
思路: 分治法
其实,这道题中,每个节点的数值是不重要的,我们可以将例子中的树的每个节点抽象成一个个小圈圈。然后:
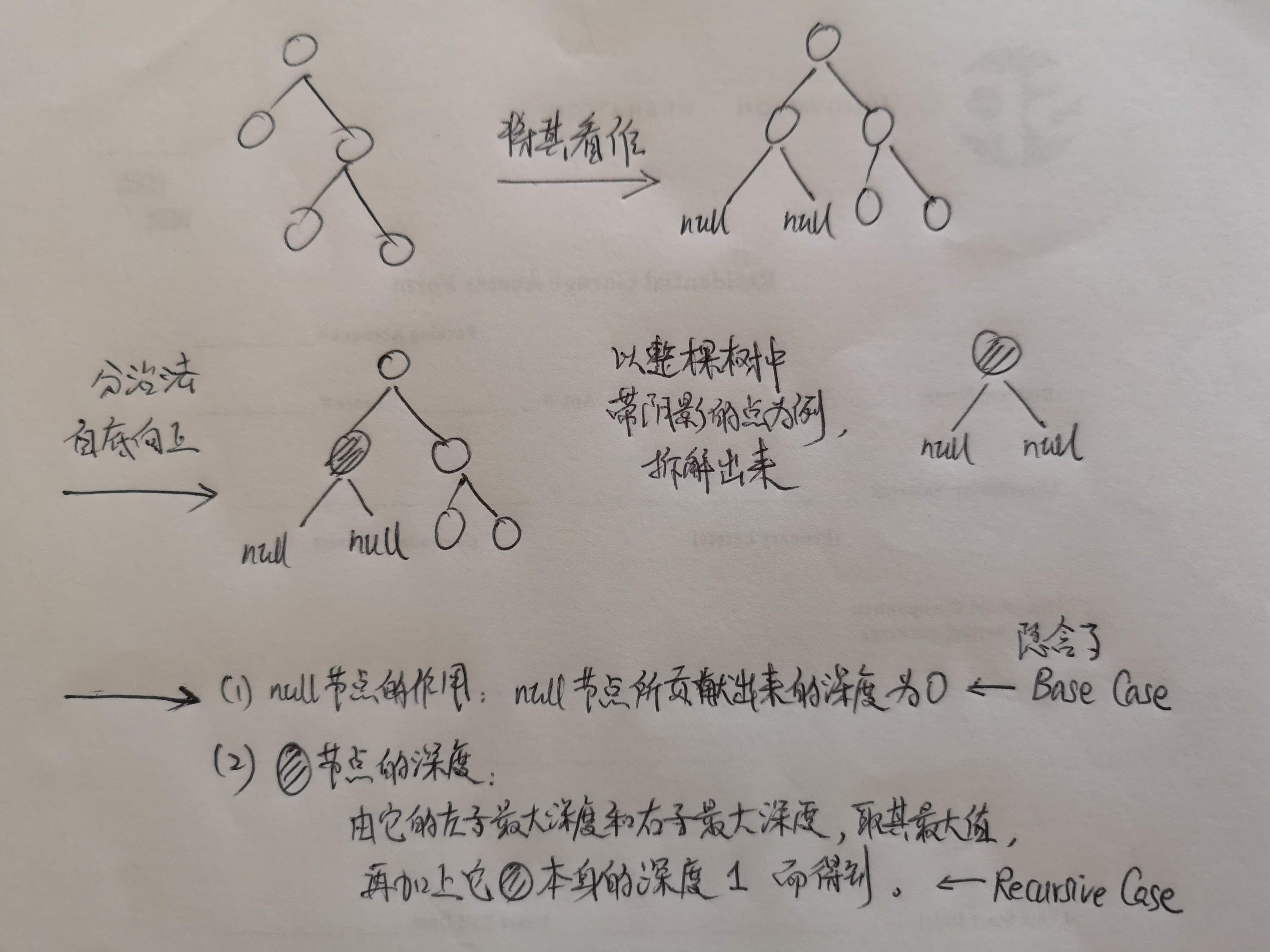
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
int left = maxDepth(root.left);
int right = maxDepth(root.right);
return Math.max(left, right) + 1;
}
}
时间与空间复杂度分析
时间复杂度,由于二叉树的每一个节点都会遍历到,所以是O(n),n为二叉树的节点个数。
空间复杂度,由于仅新开两个整数类型的变量left right来存中间计算的深度的结果,所以空间复杂度为O(1)。